Research
My research has been focused on the formulation, implementation, and advancement of statistical methodologies that are applicable across diverse fields. Specifically, my work has been devoted to developing and applying statistical methods specially designed for survival analysis, longitudinal studies, joint analysis of longitudinal and survival data, and handling of high-dimensional data.
This broad scope includes creating statistical tools that enable predictive inference from complex clustered or longitudinal data, the statistical modeling of length-biased survival outcomes and - more recently - developing techniques for variable selection, predictive inference, and multiple testing within high-dimensional datasets.
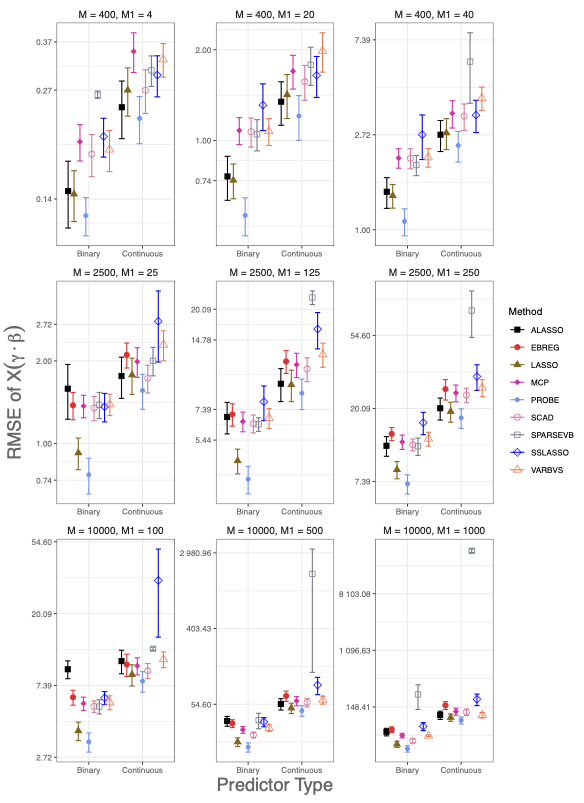
- Statistical methods for high-dimensional data. My current research has largely focused on methods to analyze data with many more predictor variables than observations. The statistical issues that arise in these analyses are simultaneously estimating the impact of a large number of predictors variables (i.e., p>n), and controlling the global error rate of the study. A focal point is interpretable machine learning models for continuous outcomes, notably sparse linear regression with high-dimensional predictors. While this is a field that has had much development over the last decade, our framework is the first option to do so with uninformative prior on the regression coefficients. Using an uninformative prior on the regression coefficients means that standard methods of performing the E-step are not possible. As a result, we take an approach that is motivated by the popular two-group approach to multiple testing, with empirical Bayes estimates of the hyperparameters. The resulting method is a computationally efficient and powerful Bayesian approach to sparse high-dimensional linear regression, with superior performance to other candidate approaches.
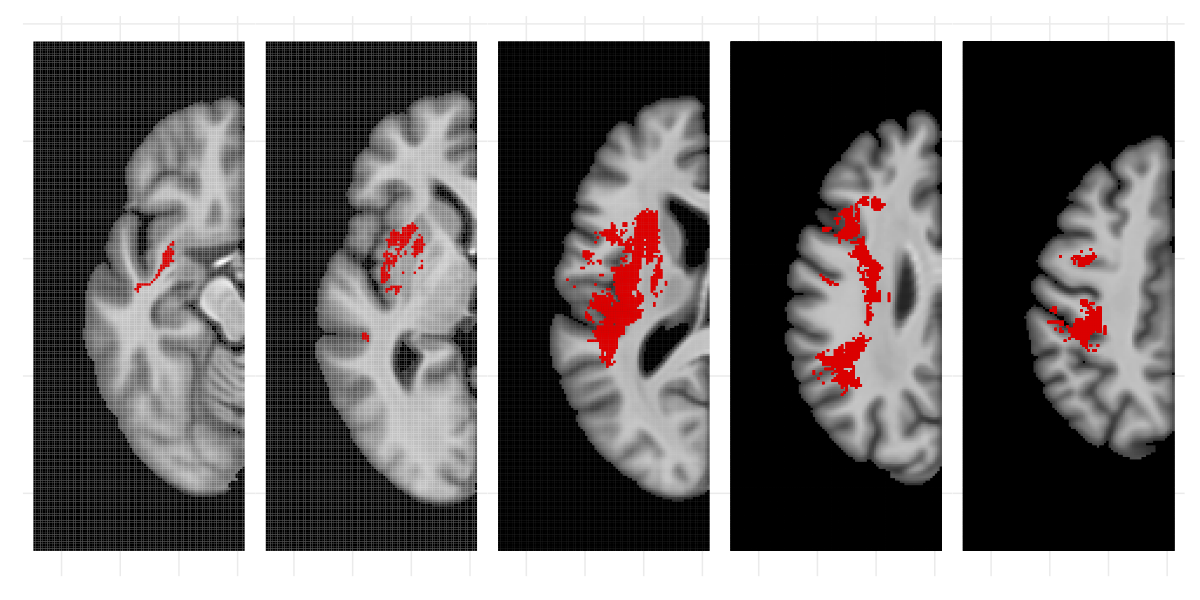
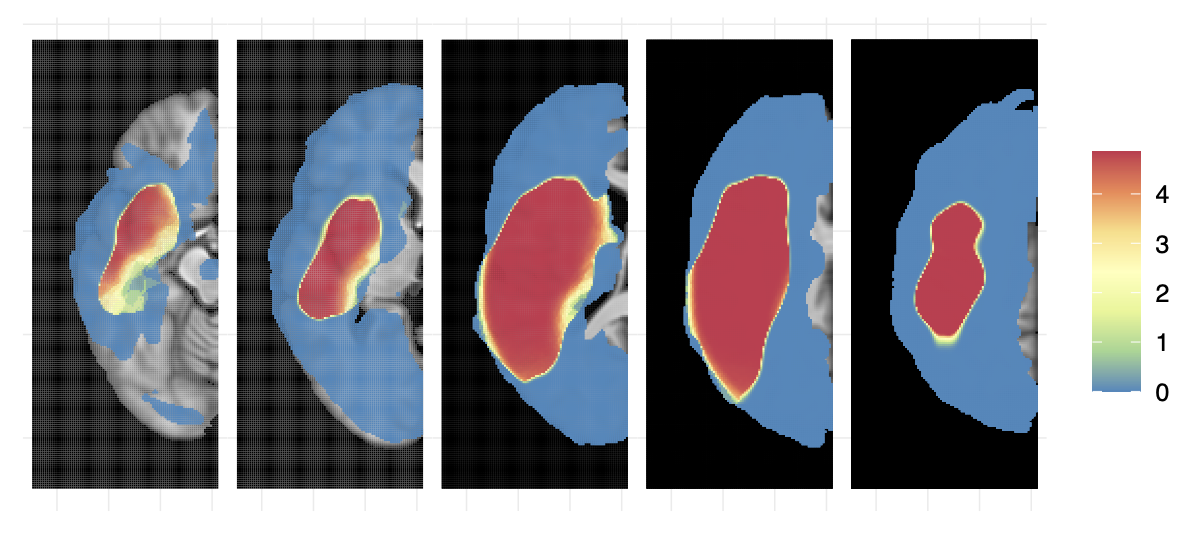
- Applications to neuroimaging data. Much of my recent methods development has been motivated by applied projects that use MRI data from patients with chronic left-hemisphere stroke and aphasia. A common goal of these studies is to use high-resolution T2-scans that indicate stroke affected areas, to map some domain of cognition to specific regions of the brain. This can provide theoretical insights regarding brain function and can also inform clinical treatment. The outcome of interest is commonly the subjects’ Aphasia Quotient (AQ), a score quantifying language impairment vital to understanding patients’ treatment options. However, collecting AQ is a cumbersome task, particularly for patients who have recently had a stroke. As a result, our methods have aimed to develop models that can predict subjects’ unknown AQ based on image data. In this research, we have been able to the quantify uncertainty in predictions from high-dimensional sprase regression models.
- Modeling and Prediction with Longitudinal/Clustered Data. My pre-tenure methodological research largely focused on joint modeling of longitudinal and survival outcomes with the application to large longitudinal cohorts. This research involved complex longitudinal models that correct for informative dropout resulting from a survival outcome. A sub-theme of this research was predicting longitudinal or survival outcomes based on observed data. From 2017 onwards, my research interests have evolved towards modeling and predictive inference for data featuring spatial-temporal dependence structures. My methodological papers in this arena predominantly involve the development of flexible longitudinal, clustered, multilevel, and/or spatial models capable of accommodating non-standard data characteristics. The emphasis lies on interpretability, valid confidence and prediction interval estimation, and adaptability to data distributions.
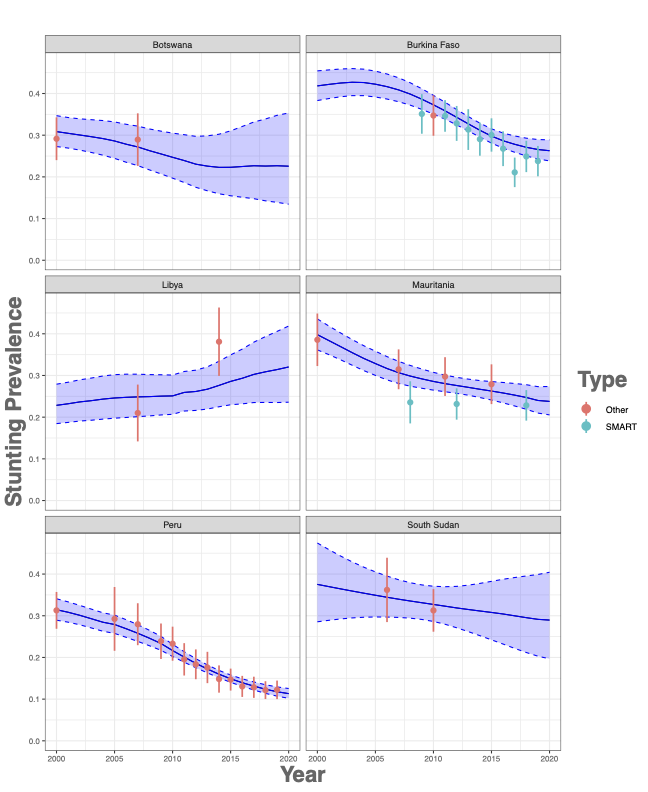
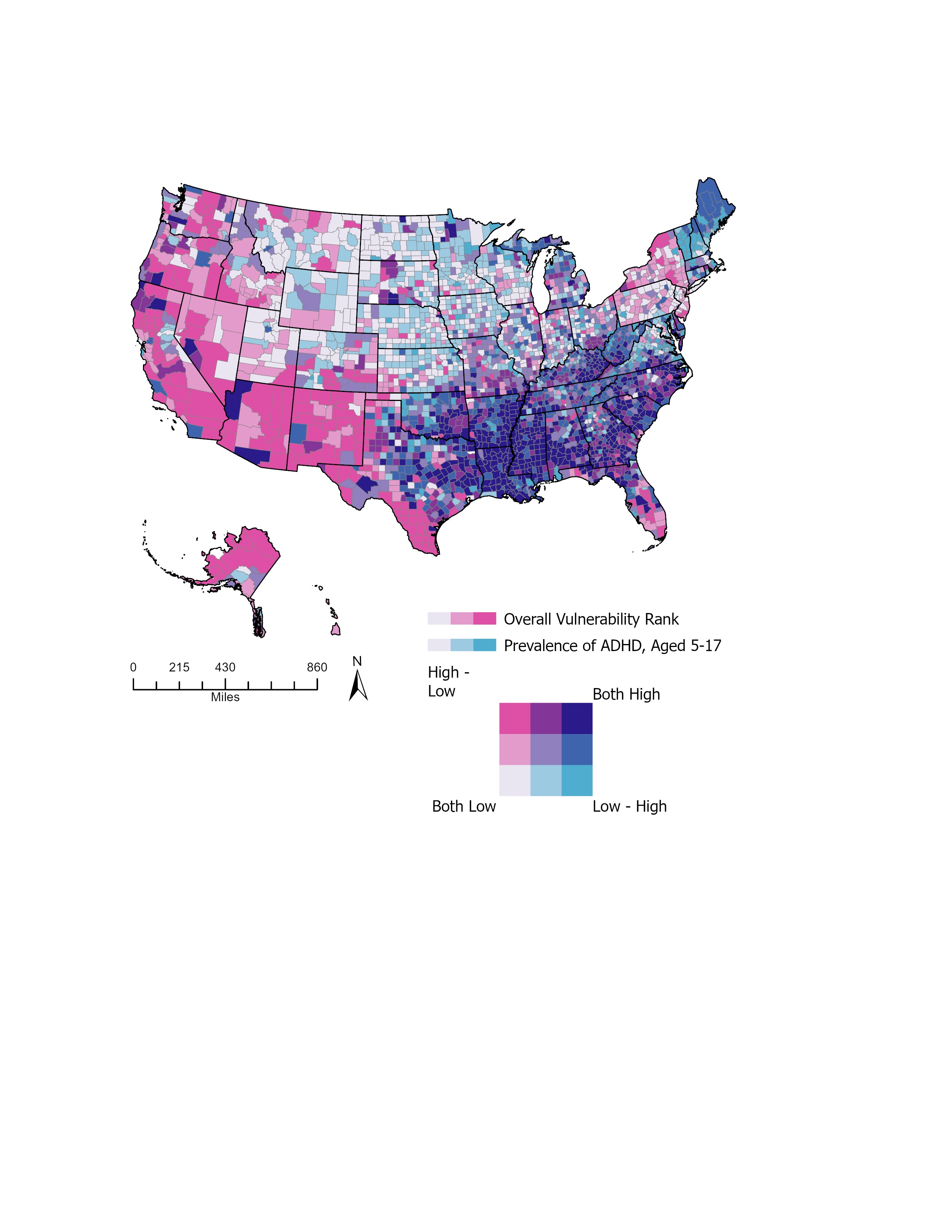
- Applications to child health. I’ve been long interested in applying statistical methodologies to the realm of child health. I have utilized various small-area estimation methods to estimate the prevalence of obesity and mental health disorders, including ADHD and ASD, in children under the age of 18. These analysis used spatial random effects model with post stratification, and we provided methods for robust measures of uncertainty quantification and multiple testing. In other research, I have led efforts into rigorous examination of physical activity, sedentary behavior, and weight status among infants and toddlers. These projects underscore my commitment to employing robust statistical approaches to tackle pressing public health issues, thereby contributing to the broader understanding and improvement of child health outcomes.
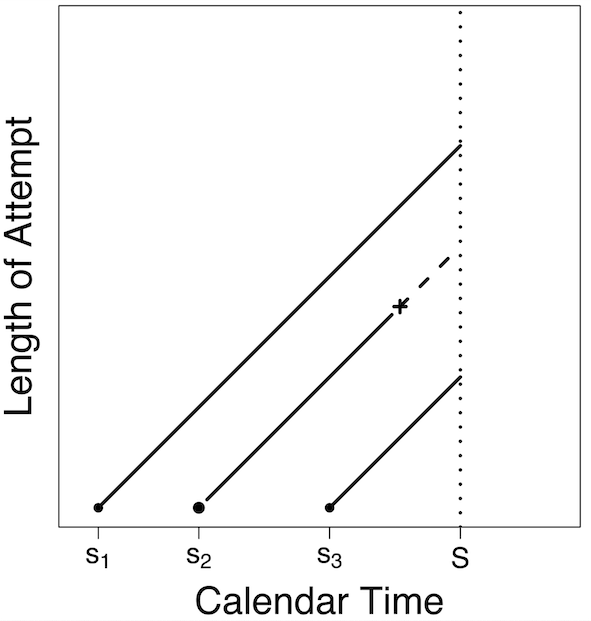
- Length Biased Survival Analysis. My research in length-biased survival analysis focuses on the development of methods for current duration data sampling, with a focus on time-to-pregnancy (TTP) and infertility. This approach is used in the National Survey of Family Growth (NSFG), where women report the duration of their ongoing pregnancy attempts. Such data are length-biased and right-censored, as longer attempts are more likely to be in progress at survey time, and complete TTP values are not available. The NSFG’s inclusion of fertility treatments adds complexity, as these alter the natural pregnancy attempt distribution and can bias TTP distribution estimates if ignored.
I currently serve as an associate editor at Statistics in Medicine and am a Statistical Consultant (reviewer) for the American Journal of Obstetrics and Gynecology.